Design and analysis of spit plot experiments

Last updated on 2020-05-26 5 min read R, Plant Breeding, agriculture, factor

Split plot design

Design and fieldbook template

In a field experiment to test for effects of fungicide on crop, treatment of fungicides may be distinguised into multiple factors – based on chemical constituent, based on formulation, based on the mode of spray, etc. In a general case scenario where two former factors could be controlled, factor combinations may be organized in several different ways. When fully crossed implementation is not possible, split plot design comes to the rescue.

It is fair to assume that fungicide constituent is relatively difficult to allocate in highly isolated patches, so we can allocate a larger plot parcel to this factor and allocate different levels of formulation to sub-plots.

The design fieldbook seems somewhat similar to that shown in Table 1.

Table 1: Split plot design with main and subplot factors in three replication blocks
plots	splots	block	trt1	trt2	mainplot
101	1	1	Mancozeb + Metalaxyl	Seed + Foliar	1
101	2	1	Mancozeb + Metalaxyl	Control	1
101	3	1	Mancozeb + Metalaxyl	Seed Treatment	1
101	4	1	Mancozeb + Metalaxyl	Foliar Spray	1
102	1	1	Trichoderma	Foliar Spray	2
102	2	1	Trichoderma	Seed + Foliar	2
102	3	1	Trichoderma	Seed Treatment	2
102	4	1	Trichoderma	Control	2

Layout plan

An example grid layout plan of the aboveshown design is shown below.

Analyis of split plot design

Let us take a grain yield dataset. The dataset contains 48 observations. Below, (in Table 2) data head have been shown after import, type-conversion and factor recoding.

Table 2: Split plot design with main and subplot factors in three replication blocks
rep	density	nitrogen	yield
1	low	1	1503
1	medium_low	1	1866
1	medium_high	1	2469
1	high	1	3786
2	low	1	2299
2	medium_low	1	1892
2	medium_high	1	3517
2	high	1	2851

Calculating variance, and setting hypothesis: A case involving single factor

In the most primitive scenario, manual calculation of variance components could just as easily be done. However, as the number of treatment factors rise, so does the complexity of computation. Manual calculation of sum of squares and the test statistic could be done as shown below. This, however, only remains valid as long as no grouping factors besides nitrogen are present, thus making it a classical scenario of single factor variance partitioning.

mu <- mean(grain_yld$yield)  # whole sample mean
ssto <- sum((grain_yld$yield - mu)^2)  # total sum of squares
mu.i <- tapply(grain_yld$yield, grain_yld$nitrogen, 
    mean)  # nitrogen(factor) means 
sstr <- sum(table(grain_yld$nitrogen) * (mu.i - mu)^2)  # nitrogen(factor) sum of squares
sse <- ssto - sstr  # error sum of squares
fstat <- (sstr/3)/(sse/45)  # F-statistic

Source	Sums of Squares	Degrees of Freedom	Mean Square	F-Stat	p-value
Treatment	6.167^{7}	3	2.056^{7}	18.465	5.925^{-8}
Error	5.01^{7}	45	1.113^{6}

\[ \begin{align*} H_0 & : \mu_1 = \mu_2 = \mu_3 \\ H_A & : \mbox{At least one pair of means not equal} \end{align*} \]

Before proceeding for an inference, It is worthwhile to be acquainted with what the distribution looks like.

Getting back to our specific split-plot design case, we develop model and generate the ANOVA table (Table 3). A split plot design is modeled with main plot factor nested within replication and a sub plot factor nested within main plot factor. This essentially partitions the main effects of replication and the main plot factor.

Table 3: Model assumption 1: ANOVA of split plot design with main and subplot factors in three replication blocks
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
rep	2	3413766	1706883	5.98	0.008
density	3	21451719	7150573	25.05	0.000
rep:density	6	6576455	1096076	3.84	0.008
density:nitrogen	12	73482134	6123511	21.45	0.000
Residuals	24	6849756	285406

Alternatively, following model specification could be made by regarding response (yield) as a product of main plot effect and sub plot effect, wherein main plot is nested inside replication (block) (ANOVA shown in Table 4).

Table 4: Model assumption 2: ANOVA of split plot design with main and subplot factors in three replication blocks
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
density	3	21451719	7150573	25.05	0.000
nitrogen	3	61673305	20557768	72.03	0.000
rep	2	3413766	1706883	5.98	0.008
density:nitrogen	9	11808829	1312092	4.60	0.001
density:rep	6	6576455	1096076	3.84	0.008
Residuals	24	6849756	285406

It should be the right time, now, to use plotting libraries and generate some beautiful graphs.

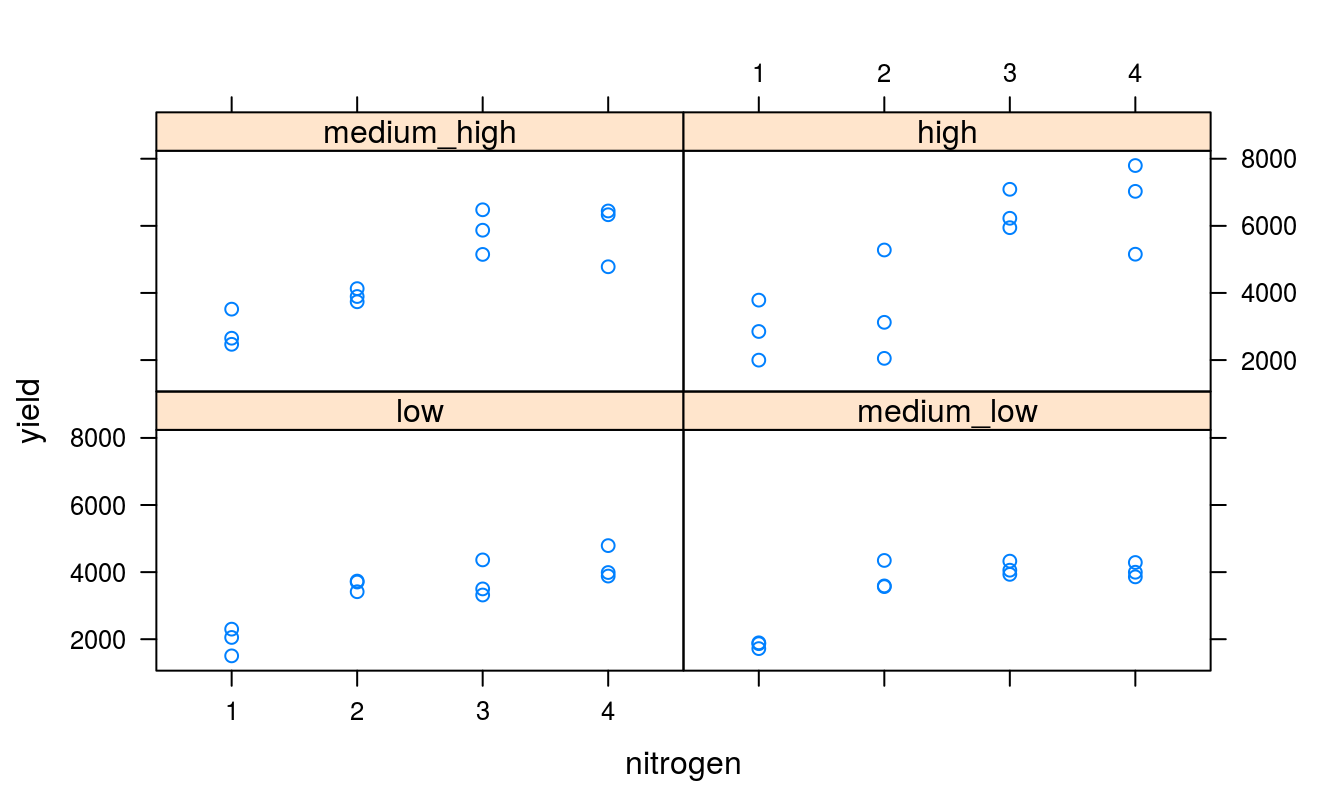
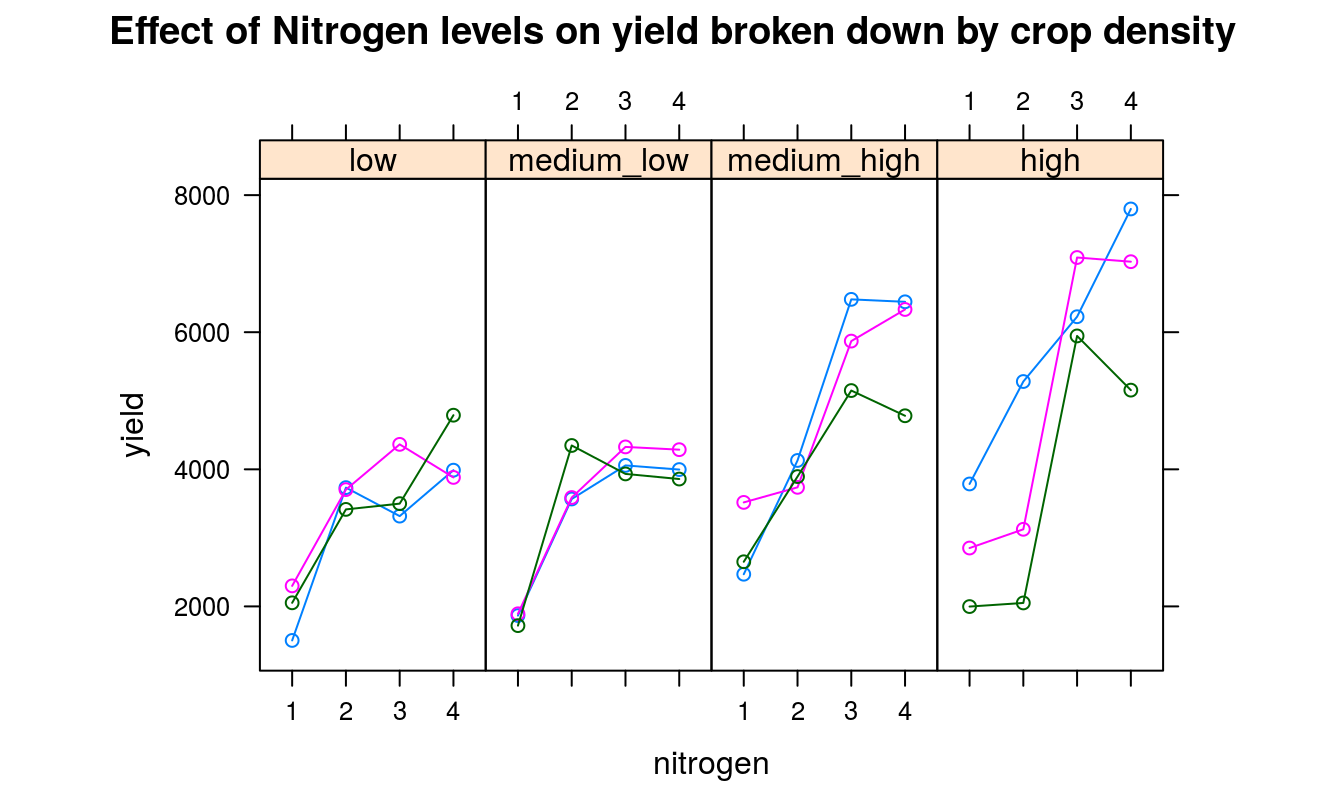
Best to take a look at some diagnostic plots now, just to make sure model assumptions and validity are not being flouted.

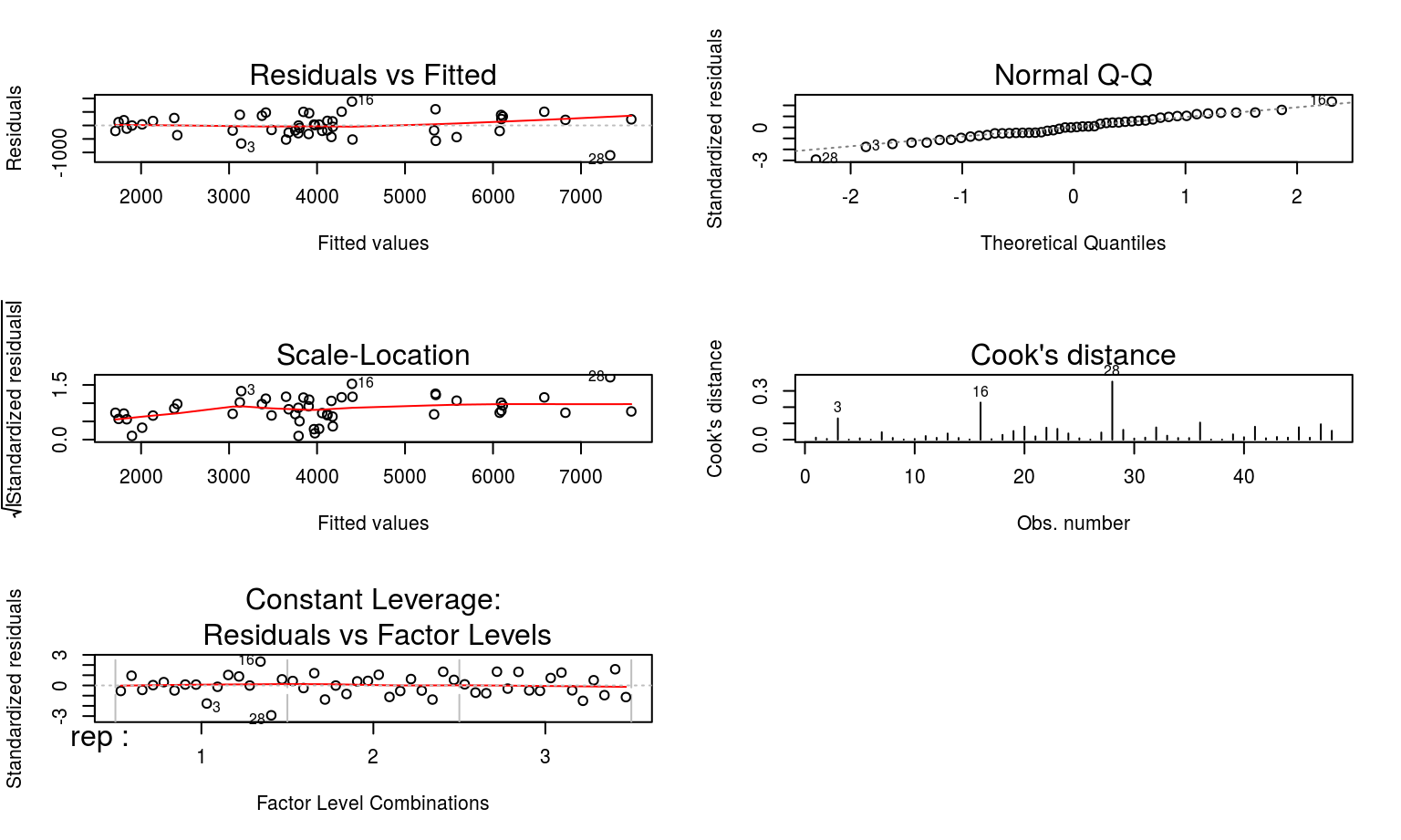
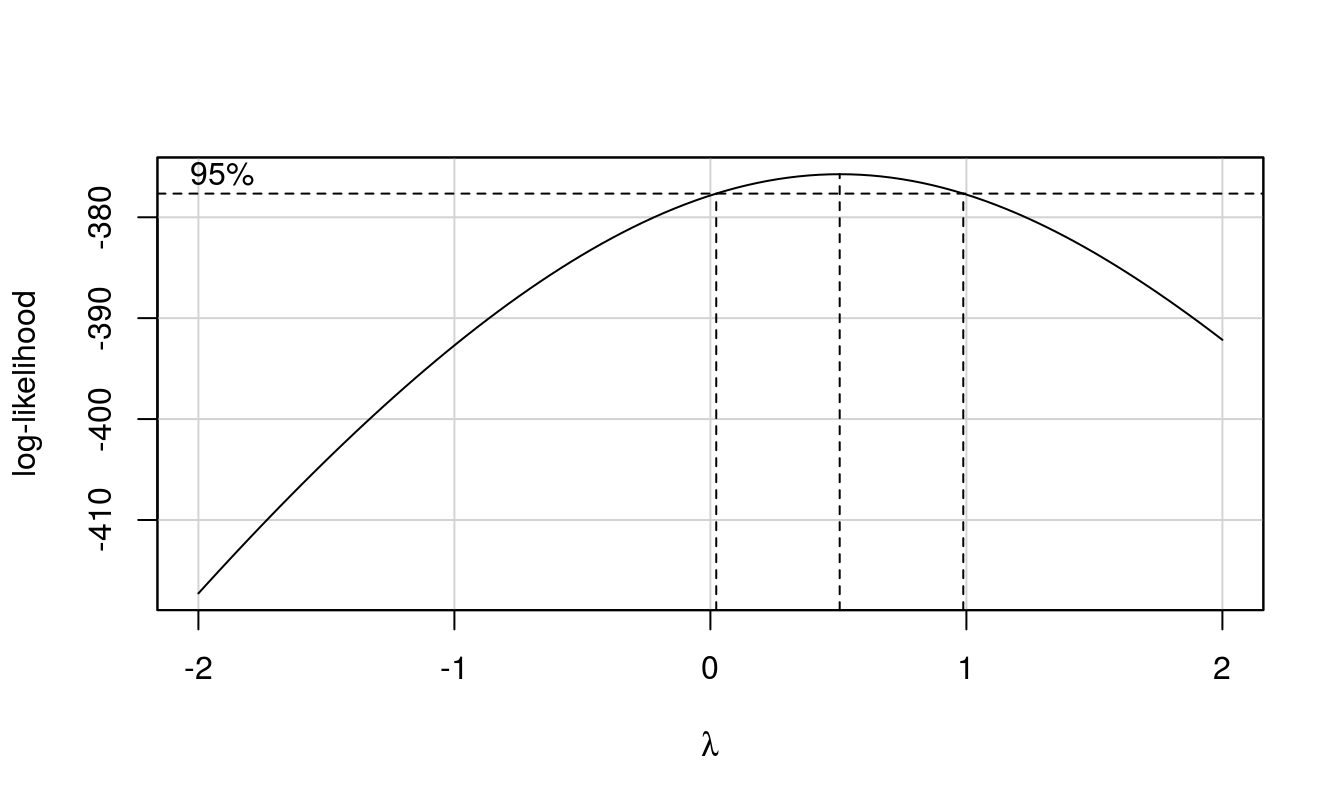
Box-Cox plots helps determine whether or not a transformation is required. To recapitulate the importance of Box-Cox plot, below is an statement quoted from http://www.itl.nist.gov/div898/handbook/eda/section3/eda336.htm, which goes:

The Box-Cox normality plot shows that the maximum value of the correlation coefficient exists at λ = (x-axis value | maximum y-axis height). The histogram of the data after applying the Box-Cox transformation(were it not indicative of normal) with λ = (x-axis value | maximum y-axis height) shows a data set for which the normality assumption is reasonable. This can be verified with a normal probability plot of the transformed data.

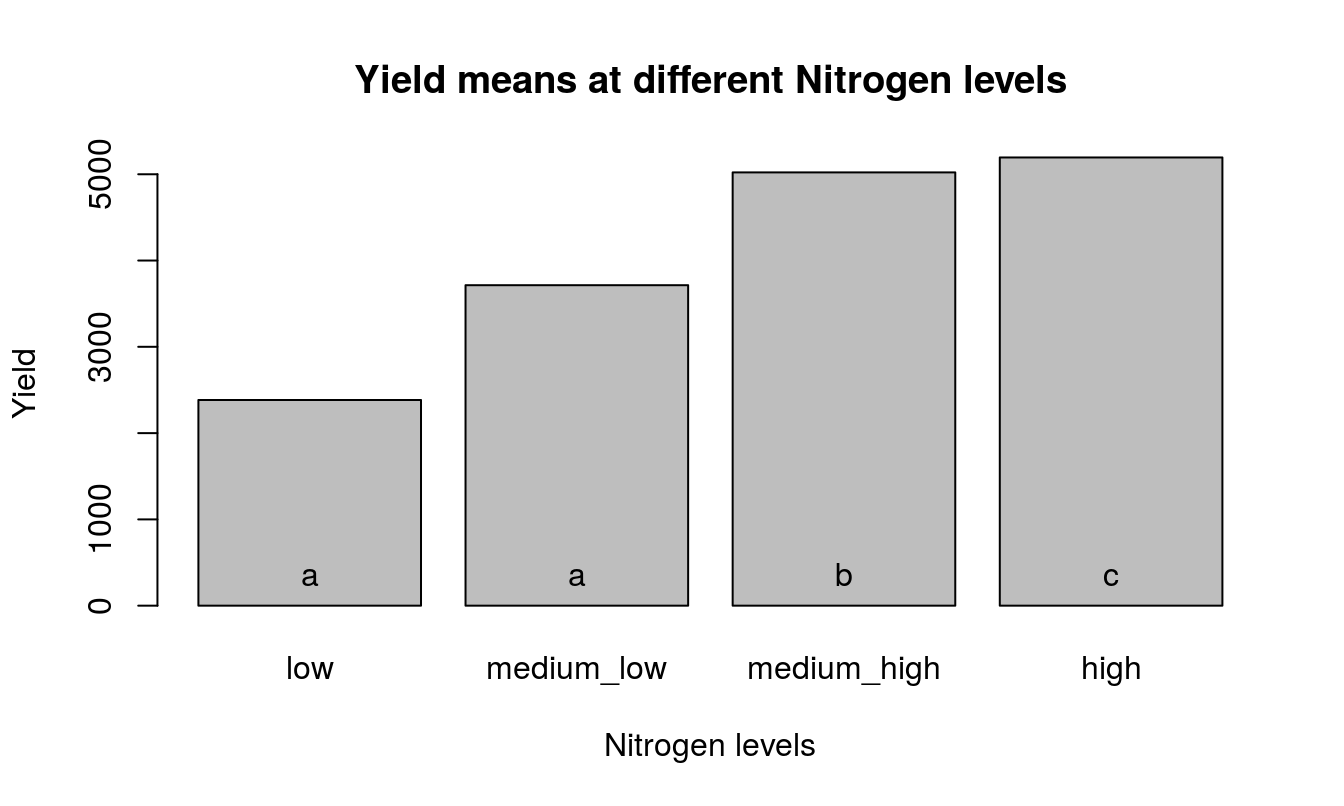
Mean separation should proceed as follows.

## 
## Study: Duncan multiple comparison among levels of nitrogen
## 
## Duncan's new multiple range test
## for yield 
## 
## Mean Square Error:  285406 
## 
## nitrogen,  means
## 
##   yield  std  r  Min  Max
## 1  2384  710 12 1503 3786
## 2  3714  757 12 2050 5281
## 3  5021 1268 12 3317 7090
## 4  5195 1367 12 3858 7798
## 
## Alpha: 0.05 ; DF Error: 24 
## 
## Critical Range
##   2   3   4 
## 450 473 487 
## 
## Means with the same letter are not significantly different.
## 
##   yield groups
## 4  5195      a
## 3  5021      a
## 2  3714      b
## 1  2384      c

Visualize the means resulting from Duncan’s test.

R agriculture